Featured Stories
September 25, 2025
PNNL Joins Space Research Group, Bringing Its Nuclear and Cybersecurity Expertise to New Heights
September 25, 2025
A Chilling Discovery: The Surprising Flexibility of Ice
September 30, 2025
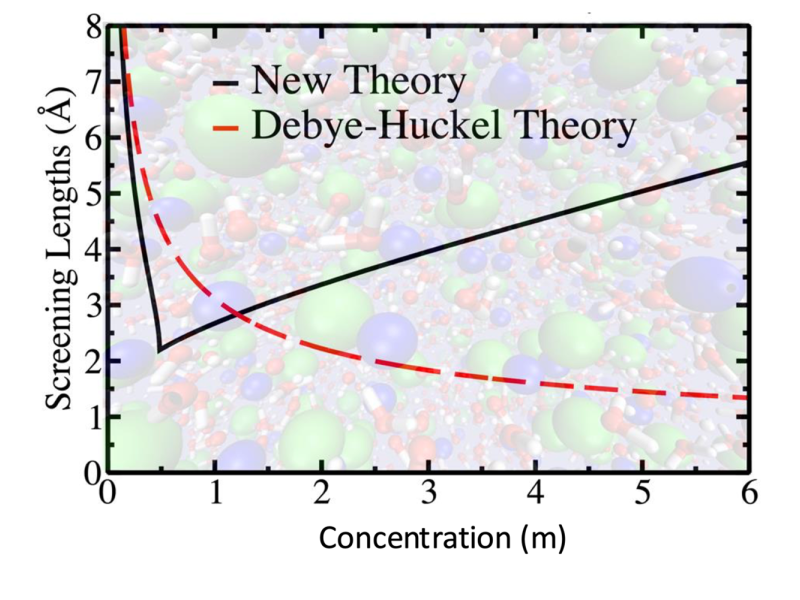
Massive Datasets Meet Their Match
September 23, 2025
At PNNL, AI Is Accelerating the U.S. Bioeconomy
Subscribe
to receive PNNL
news by email:
Latest Stories
104 results found
Filters applied: Terrestrial Aquatics, Chemical Physics, Threat-Agnostic Biodefense