By Robert S. Weber
This perspective deals with a slice of the vocabulary of heterogeneous catalysis. Michel Boudart, popularized two terms related to the title: “turnover number” [1] and its prerequisite, “dispersion” [2]. He borrowed [3] the first from enzyme catalysis where biologists [4] have long confounded counting the number of turnovers effected by an enzyme catalyst and the rate at which those turnovers occur. Following the pioneering measurements of metallic surface area by Boreskov [5], Boudart devised the second term to describe the surface/bulk ratio of the metal in supported metal catalysts. Likely, he chose to use “dispersion” because particles that are present at low areal density (i.e., that are highly dispersed) frequently exhibit a high exposure: dispersion is the means to the end.
Ultimately, he corrected the first term to “turnover rate” [6] and the terminology standards community officially [7] deprecated the second term in favor of “percentage exposure”. The first is in general use by those who study heterogeneous catalysis; the second, however, not so much.
Other authors in this issue will describe how to make the corresponding physical measurements; here I deal with why they should be made and an extension to them that may help advance the field of heterogeneous catalysis.
The measurements of exposure and rate per active center can be performed readily for homogeneous catalysts consisting of identical, molecularly defined sites that can be tracked spectroscopically around a catalytic cycle. In heterogeneous catalysis, their evaluation is more difficult but essential. Fractional exposure provides a key metric for materials that are typically prepared by procedures more akin to l’art de cuisine than stoichiometric chemical syntheses. Normalization of reaction rates into turnover rates therefore affords a basis of comparison of results and materials across laboratories, across reactions and across reaction conditions. The latter can help ensure that the reported kinetics represent intrinsic reaction rates [8-10], i.e., they are not contaminated by finite rates of mass or energy transport.
Even if a heterogeneous catalyst contains a very narrow distribution of sites, just knowing their average turnover rate and fractional exposure (or, equivalently, the average domain size) does not adequately characterize the material nor suffice to tie its activity to its structure. In heterogeneous catalysts, neither distributions of support/ligand effects nor distributions of induced heterogeneity (affinity of adsorption varying with coverage) are typically available from physical characterizations (e.g., microscopy, spectroscopy) or chemical characterizations (e.g., titration, thermal programmed desorption, SSITKA [11]). In principle, calorimetry can measure the effects of coverage but under conditions that may be unlike those employed at steady state. More subtly, the shapes of the particles, and thus the geometry of their surfaces, are not captured by exposure averaged across the particles in a sample.
To illustrate the last point, I have reanalyzed the turnover rates reported more than 30 years ago from a venture into electrochemistry by Boudart and his group [12]. That study showed that the turnover rate of electrochemical reduction of O₂ by Pt was structure sensitive—it depended strongly on the measured exposure of the particles, which was varied by changing the loading of the metal and the surface area of the support. Regrettably, that study did not present any further information about the shapes of the supported Pt particles nor even the distribution of their particle sizes.
In lieu of those actual measurements, here I have assumed that the particle size distribution W(d) can be represented by a Weibull distribution (Equation 1), which has been used to model finely divided metals [13]:
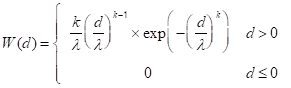
The Weibull distribution has the convenient property that it only allows for positive particle sizes. I constructed a set of Weibull distributions (Figure 1) whose means were adjusted by varying λ so as to equal the mean particle sizes reported Peuckert, et al. [12]. The exponent, k, was fixed at a value of 2. The integrals were normalized such that the mass-weighted area under each distribution (Equation 2) equaled the mass fraction of the Pt in each member, i, of the series of catalysts employed by Peuckert et al.
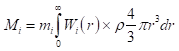
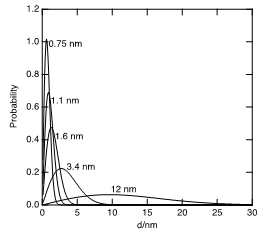
As a plausible, but admittedly speculative representation of the relevant geometry of the surfaces, I used the particle-size dependent population of 
sites for a cuboctahedron of a face-centered cubic unit cell. To facilitate interpolation and extrapolation of the population, the exact polynomials from van Hardeveld and Hartog [14], were fit to a simple power law expression in the particle diameter, d (Equation 3, Figure 2):
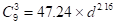
![Figure 2. Population of sites and work function as a function of the size of cuboctahedral particles of an fcc metal. Open circles: exact results calculated by van Hardeveld and Hartog [14]; solid line: Equation 3. dashed line: work function for Pt ( [15])](/sites/default/files/media/image/Figure2.png)
The integral of the Weibull distribution for each particle size multiplied by that population of sites (Equation 4) closely tracked the particle-size dependent turnover frequencies reported by Peuckert et al. [12] over the 20-fold variation in particle sizes and turnover rates (Figure 3). Remarkably, a single constant, b, sufficed to represent the rate per site presented by the particle size distributions for all the members in the series of catalysts. A plausible inference is that the activity of each particle stemmed not from the size of the particles but rather from a particular type of site they presented, perhaps the assumed sites or, at least, a feature whose particle-size dependent population paralleled their exposure. If the particle size distributions were instead represented not by Weibull distributions but rather by δ functions centered at the reported particle sizes, δ(d-dmeasured), then the comparison between estimated and measured turnover rates was close only for the smallest particles (left-most symbols in Figure 3), whose particle size distributions were narrow.
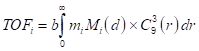
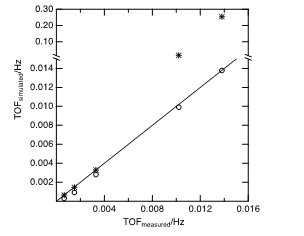
The point of this exercise is not the happy coincidence of measured and simulated turnover rates presented in Figure 3. Evidently, the close correlation depends sensitively on both assumptions—that the particle size distributions could be modeled by Weibull distributions (with k = 2) and that the kinetically significant sites tracked with the population of sites. For example, the population of other high-coordination surface sites also increase quadratically with particle size [14]. As with all of kinetics modeling, correlation does not imply causation. On the contrary, electronic features, e.g., work function and bandgaps begin to asymptotically decrease with increasing particle size at the higher values of d depicted in Figures 1 and 2 [15, 16]. Therefore, colligative “electronic effects” alone are not consistent with the observed trends in reaction rates with particle size.
Rather, the goal of this exercise is to motivate a more routine reporting of detail beyond percentage exposure. Of course, particle size distributions will depend on the conditions under which the catalyst samples are used and therefore static, pre-natal and post-mortem characterizations may not suffice. Like all of metrology, precise, accurate determination of distributions of particle sizes and shapes will involve successive approximations. But we will never succeed if we never start.
Even if we could devise characterizations that assayed the distributions of particle sizes and shapes, we would still need to contend with the possibility that the active sites may be rare [17], and, of course, dependent on the reaction catalyzed [3]. A more faithful, if less simply interpreted measure, would be the use of an ancillary, standard reaction that would sample the sites of interest and whose reaction rate would be proportional to their number. I have introduced the term fiducial reaction for that measure [18] and I and others have employed methanol oxidation [18, 19] and cyclohexane dehydrogenation [20] for normalizing the rates of related reactions. It would be valuable to see whether such an approach could be devised to normalize the rates of reactions whose kinetics depend on the formation of ensembles of sites.
The often-cited popular statistic that catalysis is involved in >80% of the value added by the chemical industry and thus about 20% of the world’s economy [21] arises largely from the importance of catalysis in the refining of petroleum and abating pollution caused by combustion of fossil fuels. The statistic will become less stark in the conceivable future when the world forsakes fossil fuels as the predominate source of energy. However, while there will then be a much-diminished demand for petroleum refining catalysts, there will still be a need for understanding the catalysis in:
- the production of chemicals and novel, highly engineered materials (e.g., battery separator membranes)
- energy conversion (electrocatalysis, photocatalysis)
- light water nuclear reactors (viz. passive autocatalytic recombiners [22])
- production and reforming of renewable fuels and energy carriers (e.g. Fischer-Tropsch catalysis of synthesis gas ex CO₂ and water; formic acid or ammonia: HCOOH➛ H₂+ CO₂; NH3➛N₂ + 3 H₂)
- emission control catalysts (combustion of even renewable fuels produces criterion pollutants: NOx, CO, unburned hydrocarbons)
The basic science needs required for those applications will continue to involve structure-activity relations, the design, synthesis, and modeling of catalysts but under conditions that may involve process conditions significantly different from those encountered in the refining of petroleum. Therefore, we will still long have the need to devise and debate methods for counting sites, mapping the surfaces of heterogeneous catalysts and normalizing reaction rates.
Acknowledgements
This work was supported by the U.S. Department of Energy, Office of Energy Efficiency and Renewable Energy, Office of Technology Transitions and the Hydrogen and Fuel Cell Technologies Office. Pacific Northwest National Laboratory is a multiprogram national laboratory operated for the US Department of Energy by Battelle under contract DE-AC05-76RL01830.
Prof. Aditya Bhan provided insightful suggestions for improving the flow of the arguments presented above.
I am grateful to Michel Boudart for patiently and generously introducing me to the international community of catalysis, starting with my “predoctoral fellowship” funded by the former US-USSR Exchange Program in Catalysis (“Bob, do you want to go to Moscow?” he asked me three years into my graduate studies). That adventure introduced me to a guest editor of this issue, Prof. Gary Haller, and other luminaries of this rich field of study. I was fortunate to overlap with much of the scientific family, LSAC, that Michel nucleated and trained at Stanford, from the periodic visits by Paul Emmett through the early days of the graduate studies of Bob Davis, the other guest editor of this issue. The help and friendship of all of them have enriched my professional and personal life.
References
[1] M. Boudart, A. Aldag, J.E. Benson, N.A. Dougharty, C.G. Harkins, On the Specific Activity of Platinum Catalysts, J. Catal., 6 (1966) 92-99.
[2] L. Spenadel, M. Boudart, Dispersion of Platinum on Supported Catalysts, J. Phys. Chem., 64 (1960) 204-207.
[3] M. Boudart, Concepts in Heterogeneous Catalysis, Interactions on Metal Surfaces., Springer, Berlin, 1975.
[4] D. Voet, J.G. Voet, Biochemistry, 2nd ed., John Wiley & Sons, New York, 1994.
[5] G.K. Boreskov, A.P. Karnaukhov, The adsorption method of measurement of the surface of platinum in platinized silica gels, Zh. Fiz. Khim, 26 (1952) 1814-1823.
[6] M. Boudart, Turnover Rates in Heterogeneous Catalysis, Chem. Rev., 95 (1995) 661-666.
[7] IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book"), 1997, accessed on: 11 May 2021.
[8] R. Davis, Turnover rates on complex heterogeneous catalysts, AIChE Journal, 64 (2018) 3778-3785.
[9] R.J. Davis, Reaction Engineering Concepts for the Catalytic Conversion of Biorenewable Molecules, in: M. Behrens, A.K. Datye (Eds.) Catalysis for the Conversion of Biomass and Its Derivatives, Max Planck Institute for the History of Science, Berlin, 2017.
[10] R.J. Madon, M. Boudart, Experimental criterion for the absence of artifacts in the measurement of rates of heterogeneous catalytic reactions, Industrial & Engineering Chemistry Fundamentals, 21 (1982) 438-447.
[11] J.G.J. Goodwin, S. Kim, W.D. Rhodes, Turnover frequencies in metal catalysis: Meanings, functionalities and relationships, in: J.J. Spivey, G.W. Roberts (Eds.) Catalysis: Volume 17, The Royal Society of Chemistry2004, pp. 320-348.
[12] M. Peuckert, T. Yoneda, R.A. Dalla Betta, M. Boudart, Oxygen Reduction on Small Supported Platinum Particles, J. Electrochem. Soc., 133 (1986) 944-947.
[13] Z. Fang, B.R. Patterson, M.E. Turner, Jr., Modeling Particle Size Distributions by the Weibull Distribution Function, Mater. Charact., 31 (1993) 177-182.
[14] R. van Hardeveld, F. Hartog, The statistics of surface atoms and surface sites on metal crystals, Surface Science, 15 (1969) 189-230.
[15] M. Seidl, K.H. Meiwes‐Broer, M. Brack, Finite‐size effects in ionization potentials and electron affinities of metal clusters, J. Chem. Phys., 95 (1991) 1295-1303.
[16] L. Zhou, M.R. Zachariah, Size resolved particle work function measurement of free nanoparticles: Aggregates vs. spheres, Chem. Phys. Lett., 525-526 (2012) 77-81.
[17] H.S. Taylor, A Theory of the Catalytic Surface, Proc. Royal Soc. A, 108 (1925) 105-111.
[18] R.S. Weber, Normalizing Hetereogeneous Electrocatalytic and Photocatalytic Rates, ACS Omega, 4 (2019) 4109-4112.
[19] L.J. Burcham, L.E. Briand, I. Wachs, E., Quantification of Active Sites for the Determination of Methanol Oxidation Turn-over Frequencies Using Methanol Chemisorption and in Situ Infrared Techniques. 2. Bulk Metal Oxide Catalysts, Langmuir, 17 (2001) 6175-6184.
[20] P.P. Silva, F.A. Silva, L.S. Portela, L.V. Mattos, F.B. Noronha, C.E. Hori, Effect of Ce/Zr ratio on the performance of Pt/CeZrO2/Al2O3 catalysts for methane partial oxidation, Catalysis Today, 107-108 (2005) 734-740.
[21] J. Hagen, Industrial Catalysis, Wiley-VCH Verlag2006.
[22] A. Rożeń, Modelling of a passive autocatalytic hydrogen recombiner – a parametric study, Nukleonika, 60 (2015) 161-169.