Accomplishments

(1) We developed two event detection methods: a) median absolute deviation-based event detection method; b) singular spectrum analysis (SSA) based change point detection approach to detect the changes of system operational conditions and identify the dominant dynamics so that proper estimators can be selected and combined to obtain the optimal performance.

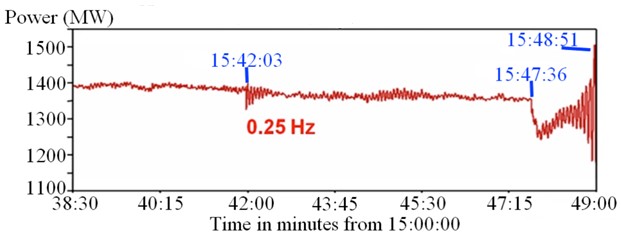
We tested the proposed event detection method through field measurement data (Fig. 1 which is in Technical Approach section) that was recorded right before a power outage happened in the western interconnection on Aug 10, 1996. The performance of the proposed approach is shown in Fig. 2. The results show that the proposed approach is able to detect the two events effectively.

Fig. 2
Fig. 2 August 10, 1996 Western Power System Breakup California-Oregon Intertie
Fig. 3
Fig. 3 Test results of the median absolute deviation based event detection method

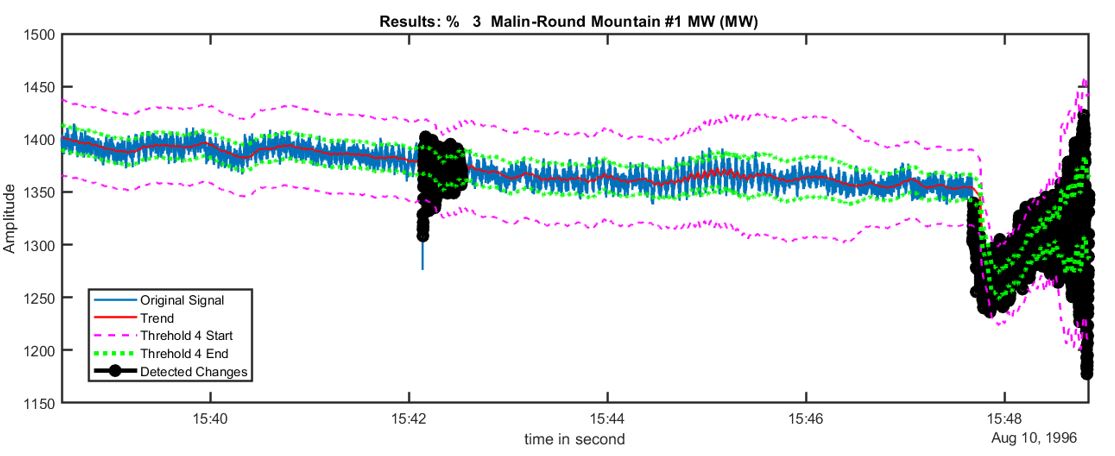
(2) We developed the interface between steady and dynamic state estimation. When state estimation switches from static state estimation to dynamic state estimation, the results of static state estimation provide the initial values for dynamic state estimation. When the state estimation switches from dynamic state estimation, the results of dynamic state estimation will provide redundant measurement for static state estimation.

To validate the effectiveness of the proposed framework in transition between SSE and DSE interchangeably, extensive simulations were carried out on the IEEE 10-machine 39-bus test system.

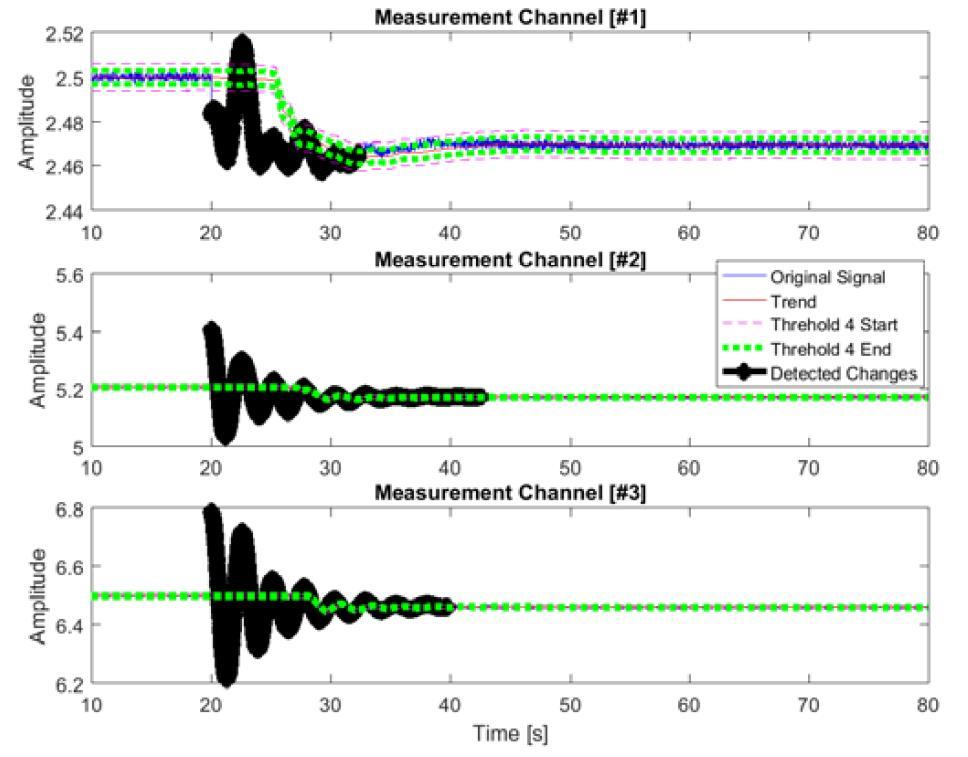
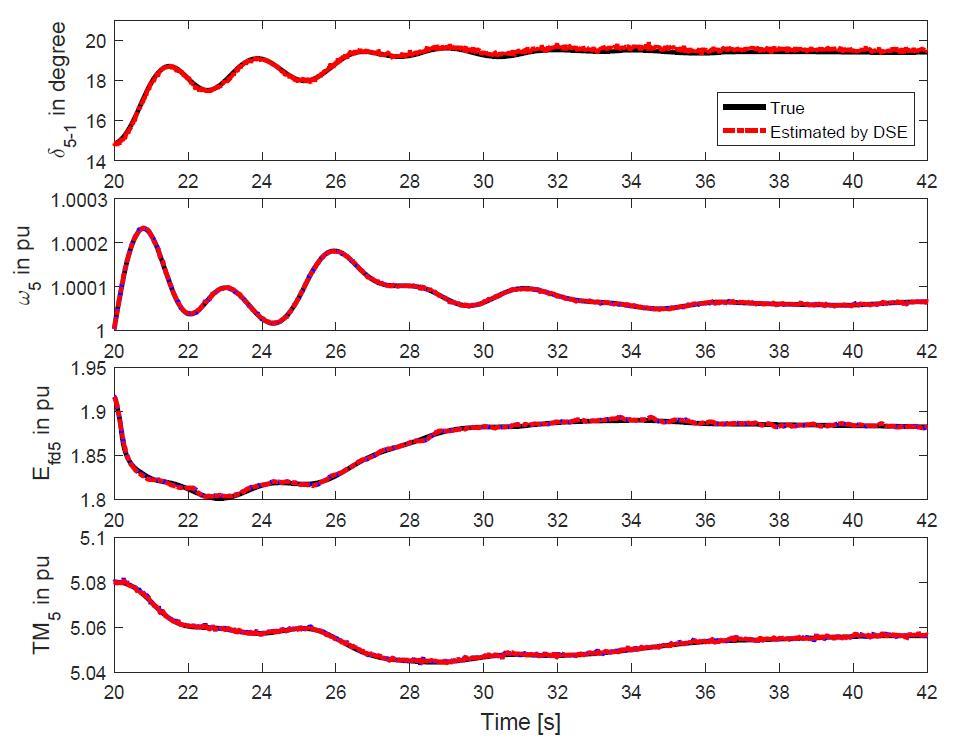
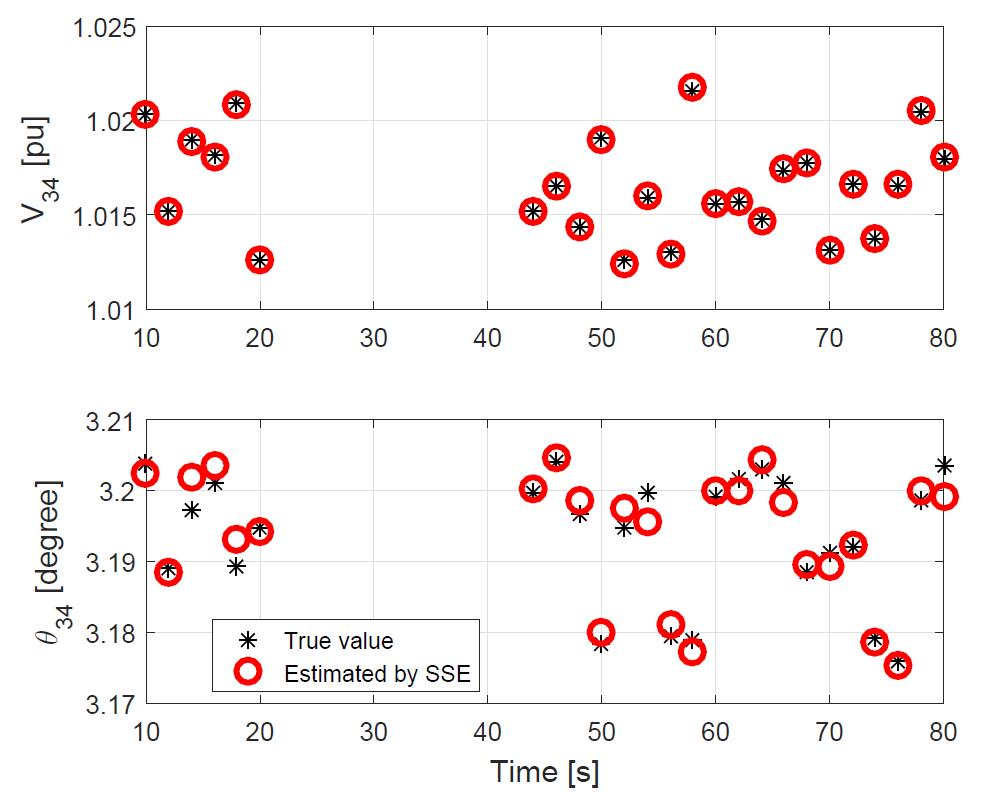
The SSA-based event detection results are shown in Fig. 4. At 20s, one line in the test system is tripped and another 70s time-domain simulations are used for test. It is observed that the transmission line tripping induced transients have been effectively detected by the SSA method. After that, the SSE results obtained at 20s are used to calculate the dynamic states for initialization and the DSE is activated. The DSE results are displayed in Fig. 5. Thanks to the good initialization, the DSE is able to track the true dynamic states of the system at the very beginning of the transient process. According to the SSA-based change point detection results, the system is operating under steady-state at 42s. Then, the DSE results are leveraged to calculate the bus voltage magnitude and angles of the system. These are used for the initialization of SSE. The estimated magnitude and angle at a specific bus are shown for illustration purpose. Its results are shown in Fig. 6. It can found that with the proper initialization via the DSE results, there is no convergence issue. Furthermore, the estimated results match the true states well. This further demonstrates the effectiveness of SSA method for system change point detection. This is because if there are undetected system changes, the non-synchronized SCADA measurements would not reflect the actual system operations and therefore, the estimated results will be far away from the true states.

EMS 2.0 Fig 4
Fig. 4. Event detection of the SSA-based method.
EMS 2.0 Fig 5
Fig. 5. DSE triggered by the SSA-based detection results at 20s.
EMS 2.0 Fig 6
Fig. 6. Voltage magnitude and angle estimation of a specific bus by the SSE, where the results from 20s to 42s are blank as it is not executed due to the transient.

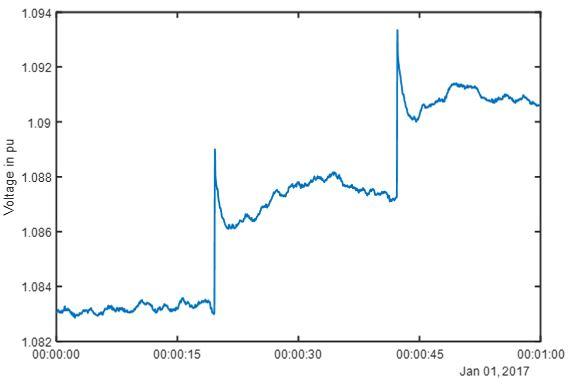
3) We applied our algorithm to a real subsystem with real PMUs measurement. An event was captured by phasor measurement shown in Fig. 7.

EMS 2.0 Fig 7
Fig. 7. An event captured by real phasor measurement

We performed DSE for the event and obtained the estimated results for a particular generator shown Fig. 8. We validated the estimated results through playback.

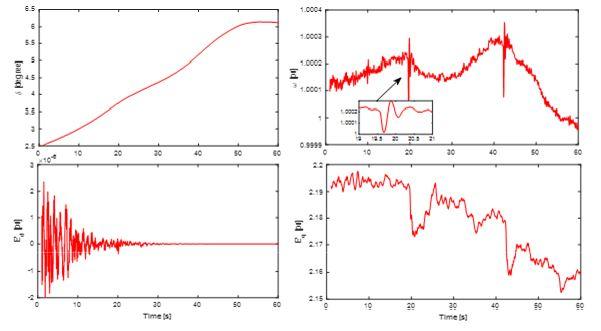
EMS 2.0 Fig 8
Fig. 8. Estimated results of DSE during the event

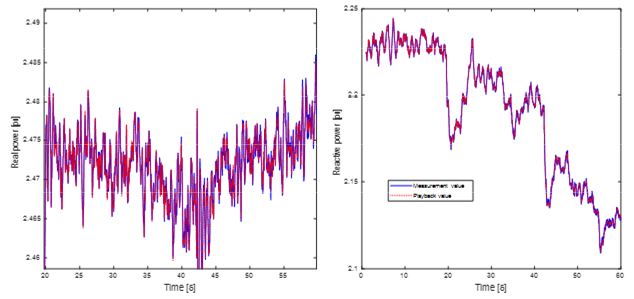
Fig. 9 shows the comparison of the measurement values and the playback values of the generator output of active power and reactive power. As can be seen from Fig. 9, the playback values can match the measurement values very well, which means the estimated values of DSE are accurate.

EMS 2.0 Fig 9
Fig. 9. Validation of the estimated values from DSE

4) Completed the testing and validation of the EMS 2.0 framework through realistic scenarios (real PMU measurement, real grid models, a subsystem of WECC shown in Fig. 10). The developed multiscale framework solved a practical issue of traditional SSE that the SSE’s performance degrades fast during disturbances and fails to capture power grid dynamics. This practical issue is recognized as a vital problem by NERC. The following video shows how the proposed framework works. As we can see from the video, before the disturbance at the time instant of t = 88s (a real event that happened on September 13, 2016), the residues are very small; and then the residue increases sharply (i.e., the SSE diverges) as the disturbance occurs, and finally, the residue and the oscillation decay return to small values.

ems fig

                                                                                      Fig. 10. A subsystem of WECC