Machine Learning Acceleration of Instanton Pathways
A new approach combining computational processes enables the more accurate simulation of nuclear quantum effects in molecular systems
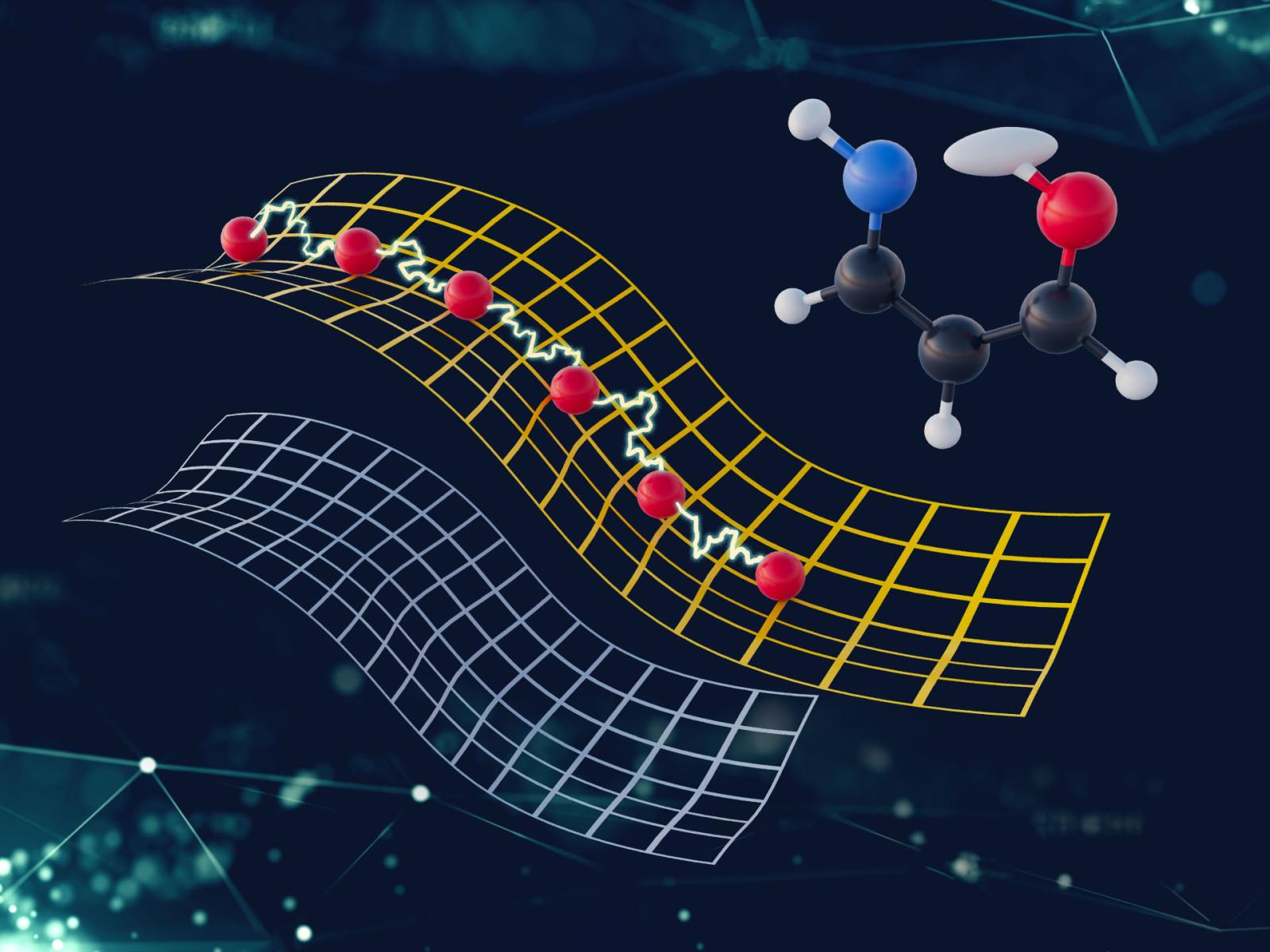
Accelerated instanton path optimization with Gaussian process regression and line integral nudged elastic band enables efficient calculation of proton tunneling rates.
(Image by Nathan Johnson | Pacific Northwest National Laboratory)
The Science
Proton transfer reactions are fundamental to biology, materials, and chemistry. While classical models offer reasonable accuracy, a precise description requires capturing nuclear quantum effects (NQEs) such as zero-point energy, tunneling, and delocalization. These effects are especially important for light nuclei like hydrogen and are essential for understanding hydrogen bonding, isotope effects, and proton transport. However, accurately modeling NQEs is computationally demanding. To address this, researchers developed a new method that combines machine learning with path integral techniques to simulate quantum tunneling efficiently and accurately in proton transfer reactions.
The Impact
The importance of proton transfer reactions spans multiple fields of science. Instanton theory, a semiclassical approach rooted in Feynman path integrals, provides a powerful framework for modeling tunneling pathways and capturing nuclear quantum effects in chemical systems. However, its application has been limited by high computational cost. By integrating machine learning into instanton-based simulations, this work reduces the cost of tunneling calculations by an order of magnitude without sacrificing accuracy. This advancement makes quantum tunneling simulations of complex systems far more practical and expands the reach of instanton theory into realistic chemical environments.
Summary
This work introduces a fast and accurate method for simulating quantum tunneling in proton transfer reactions by combining the line integral nudged elastic band approach with Gaussian process regression. The approach removes the need for costly Hessian evaluations during instanton path optimization and minimizes them during rate calculations by using machine-learned surrogate models. Benchmark simulations of representative systems show an order-of-magnitude reduction in computational cost while maintaining chemical accuracy. This advance significantly broadens the applicability of instanton theory to realistic molecular systems involving proton transfer, making it a practical tool for studying nuclear quantum effects in molecular and condensed-phase systems.
Contact
Chenghao Zhang, Pacific Northwest National Laboratory, chenghao.zhang@pnnl.gov
Niri Govind, Pacific Northwest National Laboratory, niri.govind@pnnl.gov
Funding
This work was supported by the U.S. Department of Energy (DOE), Office of Science, Basic Energy Sciences program, through the Condensed Phase and Interfacial Molecular Science program of the Chemical Sciences, Geosciences, and Biosciences division, under FWP 80818 (C.Z., N.G.), FWP 16249 (B.A.J., G.K.S.) at the Pacific Northwest National Laboratory (PNNL), and DE-SC0023249 (A.N., M.K.) at the University of Washington, Seattle. This work benefited from computational resources provided by the Environmental Molecular Sciences Laboratory, a DOE Office of Science user facility sponsored by the Biological and Environmental Research program and located at PNNL; the National Energy Research Scientific Computing Center, a U.S. Department of Energy Office of Science user facility operated under Contract No. DE-AC02-05CH11231; and PNNL’s Institutional Computing program. PNNL is operated by Battelle Memorial Institute for DOE under DOE Contract No. DE-AC05-76RL1830.
Published: September 9, 2025
C. Zhang, et al., 2025. “Accelerating Instanton Theory with the Line Integral Nudged Elastic Band Method and Gaussian Process Regression.” J. Chem. Theory Comput. 21, 15, 7517–7534. [DOI: 10.1021/acs.jctc.5c00673]