Advanced Computing, Mathematics and Data
Research Highlights
June 2015
The Reality of Problem Solving
Algorithm accounts for uncertainty to enable more accurate modeling
Results: A notable error source in modeling physical systems is parametric uncertainty, where the values of model parameters that characterize the system are not known exactly due to limited data or incomplete knowledge. In this situation, a data assimilation algorithm can improve modeling accuracy by quantifying and reducing such uncertainty. However, these algorithms often require a large number of repetitive model evaluations that incur significant computational resource costs. In response to this issue, PNNL’s Dr. Weixuan Li and Professor Guang Lin from Purdue University have proposed an adaptive importance sampling algorithm that alleviates the burden caused by computationally demanding models. In three test cases, they demonstrated that the algorithm can effectively capture the complex posterior parametric uncertainties for the specific problems being examined while also enhancing computational efficiency.
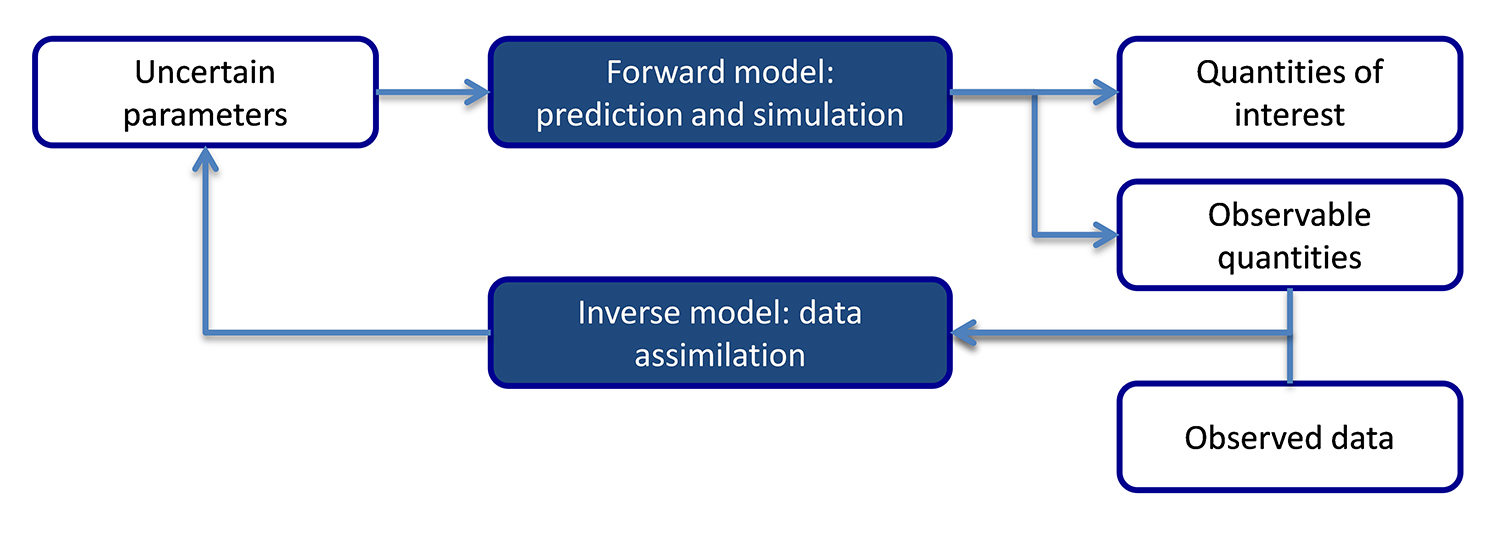
The developed algorithm takes data collected from the real system to calibrate uncertain model parameters in the complex simulator, which, in turn, leads to more accurate predictions of the quantities of researchers’ interest.
Enlarge Image.
Why it Matters: With rapid advances in modern computers, numerical models now are used routinely to simulate physical system behaviors in scientific domains ranging from climate to chemistry and materials to biology—many within DOE’s critical mission areas. However, parametric uncertainty often arises in these models because of incomplete knowledge of the system being simulated, resulting in models that deviate from reality. The algorithm developed in this research provides an effective means to infer model parameters from any direct and/or indirect measurement data through uncertainty quantification, improving model accuracy. This algorithm has many potential applications. For example, it can be used to estimate the unknown location of an underground contaminant source and to improve the accuracy of the model that predicts how groundwater is affected by this source.
Methods: Two key techniques implemented in this algorithm are: 1) a Gaussian mixture (GM) model adaptively constructed to capture the distribution of uncertain parameters and 2) a mixture of polynomial chaos (PC) expansions built as a surrogate model to alleviate the computational burden caused by forward model evaluations. These techniques afford the algorithm great flexibility to handle complex multimodal distributions and strongly nonlinear models while keeping the computational costs at a minimum level.
What’s Next? Although the algorithm works well for problems involving a small number of uncertain parameters, ongoing research with problems involving a larger number of uncertain parameters shows it is better to re-parameterize the problem, or represent it with fewer parameters, than to directly sample from the high-dimensional probability density function. Other work also involves implementing the algorithm within a sequential importance sampling framework for successive data assimilation problems. One example problem involves dynamic state estimation of power grid systems.
Acknowledgments: This material is based on work conducted under the Multifaceted Mathematics for Complex Energy Systems (M2ACS) and Collaboratory on Mathematics for Mesoscopic Modeling of Materials (CM4) projects supported by the U.S. Department of Energy’s Office of Advanced Scientific Computing Research Applied Mathematics program. Additional support was provided via a grant from the National Science Foundation. Computations were performed using Pacific Northwest National Laboratory Institutional Computing cluster systems, as well as the National Energy Research Scientific Computing Center at Lawrence Berkeley National Laboratory.
Reference:
Li W and G Lin. 2015. “An adaptive importance sampling algorithm for Bayesian inversion with multimodal distributions.” Journal of Computational Physics 294:173-190. DOI: 10.1016/j.jcp.2015.03.047.
