Advanced Computing, Mathematics and Data
Research Highlights
September 2013
Seeking Out Silent Threats to Simulation Integrity
Controlling the impact of soft errors on optimization algorithm results

After researching the impact of soft errors on large-scale computers, scientists learned the impact of the errors on algorithms is great, yet more than 95% of those soft errors can be corrected. The team found that without intervention, soft errors invalidate simulations in a significant fraction of all cases.
Results: Large-scale computing has become a necessity for solving the nation's most intractable problems. Due to their sheer number of cores, high-end computers increasingly exhibit intermittently incorrect behaviors—referred to as "soft errors"—placing the validity of simulation results at risk. A team of scientists at Pacific Northwest National Laboratory investigated the impact of soft errors on a full optimization algorithm. The team found that without intervention, soft errors would invalidate simulations in a significant fraction of all cases. They also found that 95% of the soft errors can be corrected.
The work is featured in the Journal of Chemical Theory and Computation.
Why it Matters: To deliver the 100-times performance increase relative to today's largest computers, planned systems will need to combine millions of cores. As the number of cores increases, so does the chance that some of them will intermittently produce unexpected results. These soft errors are a major impediment to utilizing the potential of upcoming high-end systems, silently corrupting the simulation data. Only by explicitly looking for such soft errors can they be detected and remedied.
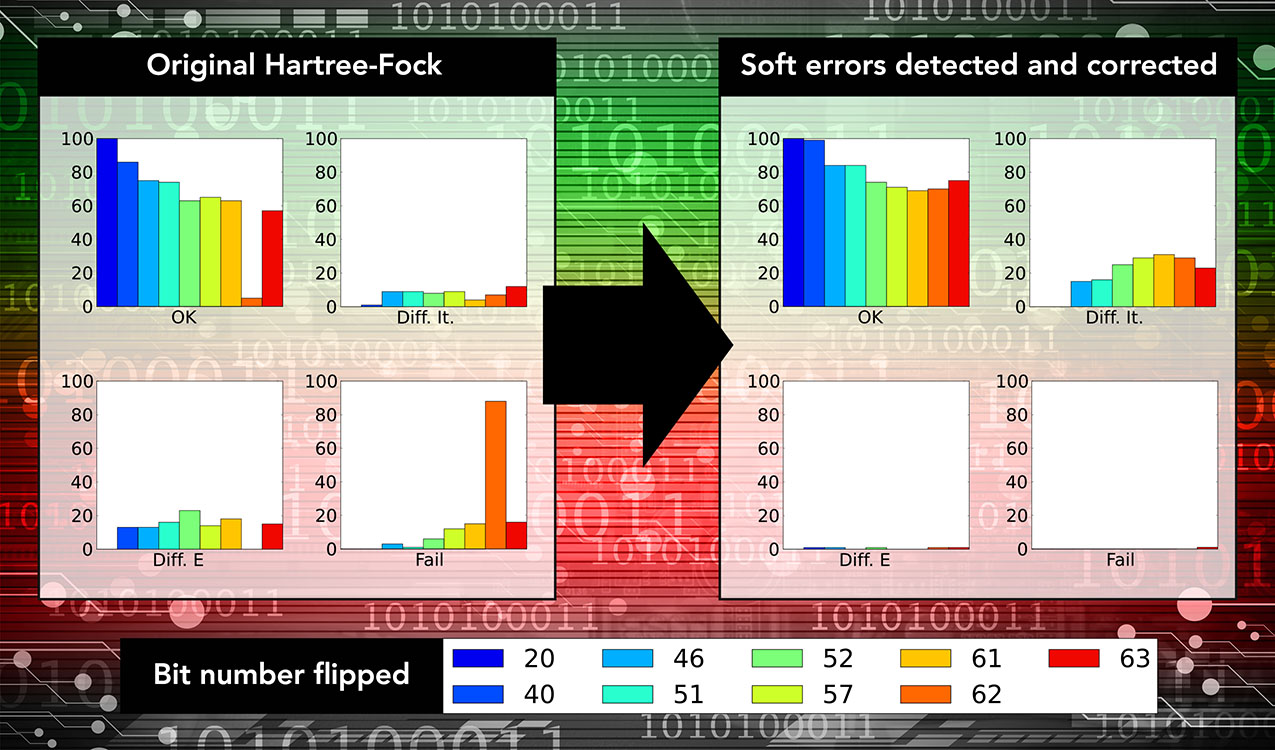
The label "OK" refers to calculations where both the total energy and number of iterations to convergence were the same as in an unperturbed calculation. "Diff. It" means that the correct energy was obtained after additional iterations. "Diff. E" means that a different energy was found, and "Fail" means that the program terminated without a converged answer. The vertical axis gives the fraction of calculations as a percentage. Each column refers to a different bit—the number of which is given in the legend. Enlarge Image
Methods: The study investigated optimization methods, which, starting from an initial guess, iteratively reduce the error until an accurate answer is reached. Because of this inherent characteristic, these methods should be relatively insensitive to uncontrolled perturbations. As a concrete example, the team explored the Hartree-Fock method of quantum chemistry. Despite the convergent characteristics of optimization methods, in general, and the Hartree-Fock method, in particular, soft errors cause calculations to fail in a significant fraction of cases. Using knowledge about the data structures, bounds and restraints can be defined, allowing large errors to be detected and corrected. In the majority of cases, the remaining residual errors are small enough that they are eliminated in the normal execution of the optimization.
What's Next? To meet growing computational requirements and solve large-scale problems, exascale computational machines are planned and expected to deliver in the next decade. Increasingly, error detection and correction will become a central consideration for any algorithm. Generic and reusable approaches to address these issues will be formulated.
Sponsors: This work was supported by PNNL's Laboratory Directed Research and Development program through the eXtreme Scale Computing Initiative. This research used resources from the Environmental Molecular Sciences Laboratory, a national scientific user facility sponsored by the Department of Energy's Office of Biological and Environmental Research and located at PNNL, as well as the PNNL Institutional Computing Facility.
Research Team: Hubertus van Dam, Abhinav Vishnu, and Bert de Jong at PNNL
Reference: van Dam HJJ, A Vishnu, and WA de Jong. 2013. "A case for soft error
detection and correction in computational chemistry." Journal of Chemical Theory and Computation, Article ASAP, July 19, 2013. DOI: 10.1021/ct400489c.
